Kareköklü Sayılar Konu Anlatımı ve Testleri
Bu içerikte kareköklerin tanımı, özellikleri ve hesaplama yöntemleri ele alınmaktadır. Kareköklerin matematikteki önemi vurgulanırken, konunun pekiştirilmesi amacıyla örnekler ve test soruları sunulmuştur. Matematiksel düşünme becerilerini geliştirmek için düzenli pratik önerilmektedir.
Kareköklü Sayılar Konu Anlatımı Ve TestleriKarekök, matematikte bir sayının kendisiyle çarpıldığında verilen sayıyı veren bir sayıdır. Karekök, genellikle √ sembolü ile gösterilir. Örneğin, √9 = 3 çünkü 3 x 3 = 9'dur. Karekökler, matematiksel işlemler ve teoriler açısından önemli bir yer tutar. Bu makalede kareköklerin tanımı, özellikleri ve çeşitli örneklerle birlikte test soruları üzerinde durulacaktır. Karekök Nedir? Karekök, bir sayının kendisiyle çarpıldığında belirli bir sonucu veren bir sayıdır. Karekök, iki farklı türde olabilir:
Karekökün Özellikleri Kareköklerin bazı temel özellikleri şunlardır:
Karekök Hesaplama Yöntemleri Karekök hesaplama yöntemleri arasında en yaygın olanları şunlardır:
Karekök Problemleri ve Örnekler Karekökler üzerine çeşitli problemler ve alıştırmalar yapmak, konunun daha iyi anlaşılmasını sağlar. İşte bazı örnekler: 1. √16 = ? - Cevap: 42. √(25 9) = ? - Cevap: 153. √(49 / 7) = ? - Cevap: 34. √(a²) = ? - Cevap: |a| Test Soruları Aşağıda, kareköklerle ilgili test soruları bulunmaktadır. Bu sorular, konunun pekiştirilmesi amacıyla hazırlanmıştır.1. √36 = ? a) 6 b) 12 c) 3 d) 182. Aşağıdaki ifadelerden hangisi doğrudur? a) √(a b) = √a + √b b) √(a / b) = √a - √b c) √(a²) = |a| d) √(0) = 13. √(64) - √(16) = ? a) 4 b) 8 c) 0 d) 64. √(x²) = ? a) x b) -x c) |x| d) x² Sonuç Karekökler, matematikte önemli bir yer tutar ve çeşitli alanlarda kullanılır. Bu makalede kareköklerin tanımı, özellikleri ve hesaplama yöntemleri üzerinde durulmuştur. Kareköklerle ilgili yapılan alıştırmalar ve test soruları, konunun pekiştirilmesine yardımcı olmaktadır. Matematiksel düşünme becerilerini geliştirmek için karekökler üzerine düzenli olarak pratik yapılması önerilmektedir. |







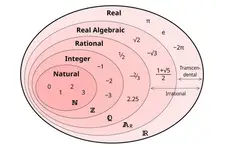





Karekök ve kök içeren sayılar hakkında paylaşılan bilgiler gerçekten ilginç. Karekökün tanımını öğrendiğimde, 4 sayısının karekökünün neden 2 olduğunu daha iyi anladım. Kök içindeki sayının üssü ile ilgili bilgiler ise, matematiksel işlemleri yaparken çok işime yaradı. Özellikle kütleli ve kuvvetli sayılarla çalışırken kütlelerinin ve kuvvetlerinin eşitlenmesi gerektiğini bilmek önemli. Köklerin türleri ve nasıl işlem yapıldığıyla ilgili örnekler, konuyu daha anlaşılır hale getirmiş. Kökler arasındaki işlemler, özellikle toplama ve çıkarma yapılırken dikkat edilmesi gereken noktalar oldukça önemli. Bu bilgileri günlük hayatımda matematiksel problemleri çözerken kullanabileceğimi düşünüyorum. Sizce, bu konuların günlük hayatta ne gibi uygulamaları olabilir?
Tulün,
Yorumun için teşekkür ederim. Matematiksel kavramların günlük hayatta nasıl kullanılabileceği üzerine düşündüğünde, bu bilgilerin ne kadar değerli olduğunu görebiliriz.
Günlük Hayat Uygulamaları
Karekök ve kök işlemlerinin pratikte birçok yeri vardır. Örneğin, inşaat sektöründe alan ve hacim hesaplamalarında sıkça kullanılır. Karekök, bir alanın kenar uzunluğunu bulmak için gereklidir. Ayrıca, mühendislik hesaplamalarında ve fiziksel problemler çözülürken bu tür matematiksel işlemler sıklıkla karşımıza çıkar.
Finansal Hesaplamalar
Finans alanında ise, faiz hesaplamalarında kök işlemleri kullanılabilir. Yatırım getirilerini hesaplarken ya da kredi ödemeleri planlanırken, bu kavramların anlaşılması faydalı olacaktır.
Günlük Problemler
Ayrıca, günlük hayatta karşılaştığımız çeşitli problemlerde, örneğin bir bahçenin büyüklüğünü hesaplamak ya da bir alanın düzenlenmesi gibi durumlarda bu matematiksel bilgi işimize yarayabilir.
Sonuç olarak, matematiksel kavramların günlük yaşamda birçok farklı alanda uygulamaları bulunmaktadır. Bu bilgileri kullanarak daha mantıklı ve hesaplı kararlar verebilirsin.