Ardışık Sayılar Konu Anlatımı ve Testleri
Ardışık sayılar, matematikte birbirini takip eden tam sayılardır ve temel matematiksel kavramların anlaşılmasında önemli bir rol oynar. Bu yazıda ardışık sayıların tanımı, özellikleri, kullanım alanları ve eğitimdeki önemi üzerinde durulmaktadır. Matematiksel işlemlerden istatistiksel analize kadar geniş bir yelpazede yer alan ardışık sayılar, temel becerilerin geliştirilmesine katkı sağlar.
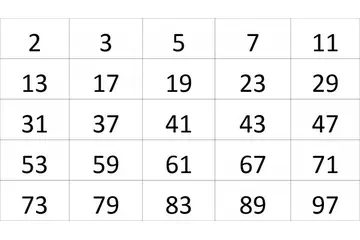
Ardışık Sayılar Ardışık sayılar, matematikte bir dizinin ardışık elemanlarıdır ve genellikle birbirini takip eden pozitif veya negatif tam sayılar olarak tanımlanır. Bu sayılar, aralarındaki farkın sabit olduğu bir dizi oluştururlar. Ardışık sayıların temel özellikleri ve kullanımları, matematiksel işlemlerden istatistiksel analizlere kadar geniş bir yelpazeyi kapsar. Bu makalede, ardışık sayıların tanımı, özellikleri, örnekleri ve testleri üzerinde durulacaktır. Ardışık Sayıların Tanımı Ardışık sayılar, matematikte birbirini takip eden tam sayılardır. Örneğin, 1, 2, 3 veya -2, -1, 0 gibi diziler ardışık sayılar dizisine örnektir. Bu sayılar genellikle n, n+1, n+2 şeklinde tanımlanır; burada n bir tam sayıdır. Ardışık Sayıların Özellikleri Ardışık sayıların bazı temel özellikleri şunlardır:
Bu özellikler, ardışık sayıların matematiksel analizlerde ve hesaplamalarda kullanılmasını kolaylaştırır. Ardışık Sayıların Kullanım Alanları Ardışık sayılar, çeşitli matematiksel kavramların yanı sıra günlük yaşamda da kullanılmaktadır. İşte bazı kullanım alanları:
Ardışık Sayılarla İlgili Testler Ardışık sayılarla ilgili çeşitli matematiksel testler ve problemler, öğrencilerin matematiksel düşünme becerilerini geliştirmeye yardımcı olur. İşte bazı temel test örnekleri:
Bu testler, öğrencilere ardışık sayıların özelliklerini anlamalarına yardımcı olur ve pratik yapmalarını sağlar. Sonuç Ardışık sayılar, matematiksel kavramların temelini oluşturan önemli bir konudur. Tanımları, özellikleri ve kullanım alanları ile birlikte, bu sayılar birçok matematiksel problemde karşımıza çıkar. Öğrencilerin ardışık sayılarla ilgili testler çözmesi, bu konudaki kavrayışlarını derinleştirecek ve matematiksel düşünme becerilerini geliştirecektir. Ekstra Bilgiler Ardışık sayılar, sadece pozitif tam sayılarla sınırlı değildir. Negatif ardışık sayılar da mevcuttur. Ayrıca, ardışık sayıların toplamı formülü:\[\text{Toplam} = \frac{n}{2} \times (\text{ilk terim} + \text{son terim})\]şeklindedir. Burada n, toplam terim sayısını ifade eder. Bu formül, ardışık sayılarla ilgili yapılan hesaplamalarda oldukça faydalıdır. Bu makale, ardışık sayıların matematikteki önemini ve çeşitli yönlerini kapsamlı bir şekilde ele almıştır. Matematiksel düşünme yeteneği geliştirmek için ardışık sayılar üzerinde çalışmak, öğrencilerin analitik becerilerini artırmalarına yardımcı olacaktır. |


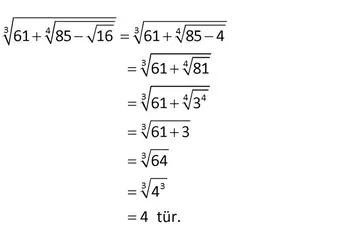





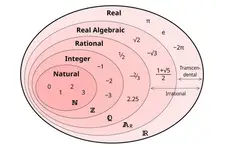





Ardışık tam sayıların örneğinde, sayıların negatiften pozitife doğru gittiğini fark ettim. Bu sayıların her iki tarafa doğru sınırsız olduğunu söyleyebilir miyiz?
Evet, Havva, ardışık tam sayılar negatiften pozitife doğru giderken her iki tarafa da sınırsız bir şekilde devam eder. Bu yüzden ardışık tam sayılar, negatif sonsuzdan pozitif sonsuza kadar uzanır diyebiliriz.