Tek ve Çift Sayılar Konu Anlatımı ve Testleri
Tek ve çift sayılar, matematikte temel bir kavramdır. Bu yazıda, bu sayıların tanımları, özellikleri ve aralarındaki ilişkiler detaylı bir şekilde incelenecek, ayrıca konuyla ilgili test soruları ve uygulamalar sunulacaktır. Matematiksel düşünme becerilerini geliştirmek için önemli bir kaynak niteliğindedir.
Tek ve Çift Sayılar Tek ve çift sayılar, matematiğin temel kavramlarından biridir ve sayıların sınıflandırılmasında önemli bir yer tutar. Bu makalede, tek ve çift sayıların tanımları, özellikleri ve aralarındaki ilişkiler detaylı bir şekilde ele alınacak, ayrıca bu konu ile ilgili testler ve örnekler sunulacaktır. Tek Sayılar Tek sayılar, 2'ye tam bölünemeyen, yani 2 ile bölümünden kalan 1 olan sayılardır. Matematiksel olarak, bir sayının tek olduğunu belirlemek için aşağıdaki formül kullanılabilir:- n = 2k + 1, burada k herhangi bir tam sayıdır. Özellikleri:
Çift Sayılar Çift sayılar, 2'ye tam bölünebilen, yani 2 ile bölümünden kalan 0 olan sayılardır. Matematiksel olarak, bir sayının çift olduğunu belirlemek için aşağıdaki formül kullanılabilir:- n = 2k, burada k herhangi bir tam sayıdır. Özellikleri:
Tek ve Çift Sayılar Arasındaki İlişki Tek ve çift sayılar arasında belirli bir ilişki bulunmaktadır. Örneğin:- İki tek sayının toplamı çift bir sayıdır.- İki çift sayının toplamı çift bir sayıdır.- Bir tek sayının ve bir çift sayının toplamı tek bir sayıdır. Bu ilişkiler, sayıların toplama ve çarpma işlemleri sırasında dikkate alınmalıdır. Testler ve Uygulamalar Tek ve çift sayılar ile ilgili çeşitli testler ve alıştırmalar, öğrencilerin bu kavramları daha iyi anlamalarına yardımcı olabilir. Aşağıda bazı örnek test soruları verilmiştir: Test Soruları:
Sonuç Tek ve çift sayılar, matematiğin temel taşları arasında yer alır. Bu kavramların anlaşılması, daha karmaşık matematiksel işlemlerin ve teorilerin öğrenilmesinde önemli bir rol oynar. Öğrencilerin bu konuyu pekiştirmek için çeşitli alıştırmalar yapması önerilmektedir. Bu makalede tek ve çift sayılar hakkında detaylı bilgi verilmiştir. Bu bilgiler, öğrencilere matematiksel düşünme becerilerini geliştirme ve sayıların özelliklerini anlama konusunda yardımcı olacaktır. |


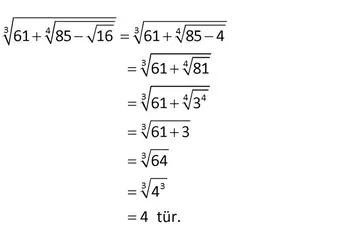





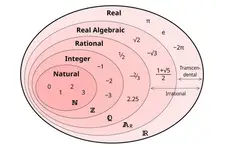





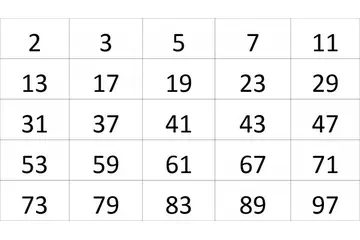
Matematikte tek ve çift sayıların durumu gerçekten ilginç. Özellikle asal sayılarla olan ilişkisi dikkat çekici. Tek sayılar arasında 2 dışında asal sayı yokken, bu durum çift sayılar için de geçerli. Aslında, tek sayıların asal olma durumu, matematiksel yapının ne kadar katmanlı olduğunu gösteriyor. İki tek sayının toplamı veya farkının neden her zaman çift olduğunu düşünmek bile matematikteki basit ama derin kuralların bir örneği. Ayrıca, çarpma işlemlerinin sonuçlarıyla ilgili kurallar da oldukça mantıklı. Bir sayı ile çarpıldığında çift veya tek olma durumu, sayılar arasındaki ilişkiyi anlamamıza yardımcı oluyor. Paritenin matematikteki önemi ve sayılar arasındaki denklik ilişkisi de oldukça etkileyici. Sizce bu tür matematiksel yapılar, günlük yaşamda nasıl bir rol oynuyor?
Zaid,
Matematik ve Günlük Hayat
Matematikteki temel yapılar, günlük yaşamda birçok alanda karşımıza çıkıyor. Özellikle sayılar arasındaki ilişkiler, finansal hesaplamalardan mühendislik tasarımlarına kadar geniş bir yelpazede uygulama buluyor. Örneğin, bütçe yönetiminde harcama ve gelirlerin takibi, çift ve tek sayıların özelliklerini anlamamıza yardımcı olabilir.
Asal Sayılar ve Güvenlik
Asal sayıların özel durumu, özellikle bilgisayar bilimlerinde şifreleme yöntemlerinde önemli bir yere sahip. Bu sayılar, verilerin güvenliğini sağlamak için kullanılıyor. Dolayısıyla, matematikteki bu tür yapılar, bilgi güvenliğinden veri analizi gibi alanlara kadar birçok pratik uygulama sunuyor.
Matematiksel Düşünme ve Problem Çözme
Ayrıca, matematiksel düşünme becerileri, günlük hayatta karşılaştığımız problemleri çözmemizi kolaylaştırıyor. Basit matematik kurallarıyla mantıklı ve sistematik bir şekilde düşünmek, karar verme süreçlerimizi etkileyebilir.
Sonuç olarak, matematikteki bu yapılar, hem teorik olarak ilginç olduğu kadar, pratikte de önemli roller üstleniyor. Bu tür matematiksel kavramların günlük yaşamda nasıl bir etkisi olduğunu görmek, matematiğin her alanda ne kadar temel bir rol oynadığını gösteriyor.