Üslü Sayılar Konu Anlatımı ve Testleri
Üslü sayılar, matematikte bir sayının kendisiyle kaç kez çarpılacağını gösteren ifadelerdir. Bu kavram, matematiksel işlemleri kolaylaştırır ve birçok bilim dalında kullanılır. Üslü sayıların tanımı, özellikleri ve pratik test soruları ile konunun temelleri ele alınmaktadır.
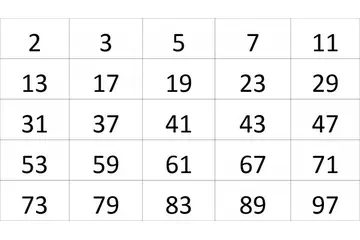
Üslü sayılar, matematikte bir sayının kendisiyle kaç kez çarpılacağını gösteren bir ifadedir. Üslü sayılar, matematiksel işlemlerin daha kolay ve etkili bir şekilde yapılmasını sağlar. Bu yazıda, üslü sayılara dair temel kavramlar, özellikler ve test soruları üzerinde durulacaktır. Üslü Sayı Nedir?Üslü sayı, a^n şeklinde ifade edilen bir matematiksel ifadedir; burada "a" taban, "n" ise üst sayıdır. Taban, çarpma işlemini gerçekleştireceğimiz sayıyı, üst ise bu tabanın kaç kez kendisiyle çarpılacağını belirtir. Örneğin, 2^3 ifadesinde 2 tabanı 3 kez kendisiyle çarpılır ve sonuç 8'dir. Üslü Sayıların Özellikleri Üslü sayıların bazı temel özellikleri şunlardır:
Üslü Sayıların Kullanım Alanları Üslü sayılar, matematiksel hesaplamalarda ve çeşitli bilim dallarında yaygın olarak kullanılır. Başlıca kullanım alanları:
Test Soruları Aşağıda, üslü sayılar konusunu pekiştirmek için birkaç test sorusu yer almaktadır: 1. 3^4 işleminin sonucu nedir? - A) 9 - B) 27 - C) 81 - D) 642. 5^3 5^2 işleminin sonucu hangi üslü sayı ile ifade edilir? - A) 5^5 - B) 5^6 - C) 5^7 - D) 5^83. (2^3)^2 işleminin sonucu nedir? - A) 4 - B) 8 - C) 16 - D) 64 Sonuç Üslü sayılar, matematiksel işlemlerin temel taşlarından birini oluşturmakta ve geniş bir uygulama alanı bulmaktadır. Bu yazıda, üslü sayıların tanımı, özellikleri, kullanımları ve test sorularına dair bilgiler sunulmuştur. Öğrencilerin ve ilgililerin, bu konudaki temel bilgileri pekiştirmeleri, ileride daha karmaşık matematiksel kavramları anlamalarına yardımcı olacaktır. |


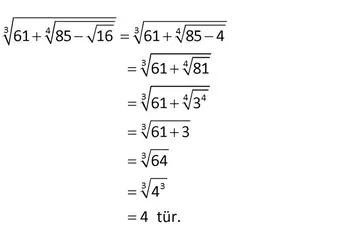










Bu üslü sayılar konusunu okuduğumda, gerçekten de matematikteki önemini anlıyorum. Özellikle öğrencilerin bu konuyu öğrenmeleri, matematiksel düşünme becerilerini geliştirmelerine büyük katkı sağlıyor. Üslü sayının tanımını yaparken, bir sayının kendisiyle çarpımını anlamak çok önemli. Peki, üslü sayılarda negatif sayılarla çalışmanın zorlukları hakkında daha fazla bilgi verebilir misin? Özellikle çift ve tek üslü durumları arasındaki farklar neler?
Zeyneb Hanım,
Üslü Sayıların Önemi
Üslü sayılar, matematikte oldukça önemli bir yere sahiptir. Özellikle öğrencilere matematiksel düşünme becerilerini kazandırmak ve sayıların büyüklüklerini daha kolay ifade edebilmek açısından büyük fayda sağlar.
Negatif Sayılarla Çalışmanın Zorlukları
Negatif sayılarla üslü sayılar üzerinde çalışmak, bazı karmaşık durumları beraberinde getirebilir. Örneğin, negatif bir sayının çift bir üslü ile yükseltilmesi durumunda sonuç her zaman pozitif olurken, tek bir üslü ile yükseltildiğinde sonuç negatif olur. Bu durum, öğrencilerin kavramları anlamada zorluk çekmesine yol açabilir.
Çift ve Tek Üslü Durumlar
Çift üslü sayılarda, negatif bir sayının sonucu pozitif olduğu için, bu durum genel olarak daha anlaşılır ve tahmin edilebilir bir sonuç sunar. Ancak tek üslü sayılarda negatif bir sayının sonucu negatif olduğu için, öğrencilerin bu durumu kavraması daha zor olabilir. Bu nedenle, öğrencilerin her iki durumu iyi anlamaları ve pratik yapmaları önemlidir.
Sonuç olarak, üslü sayılar üzerinde çalışırken, negatif sayılarla olan etkileşimleri anlamak için derin bir bilgiye sahip olmak ve bolca pratik yapmak gereklidir. Bu, hem kavramları pekiştirecek hem de matematiksel düşünme becerilerini geliştirecektir.